Les Pentagones Mystérieux

Les Hexagones, ça va ...

Dans la section peut-on paver on a vu que les triangles et les quadrilatères peuvent toujours paver le plan et que les polygones convexes avec plus de sept arêtes ne peuvent jamais paver le plan.

Si l'on regarde les polygones convexes, il nous reste donc à étudier que les hexagones et les pentagones.

Pas tous les hexagones peuvent paver le plan, mais on sait classifier les hexagones qui peuvent le faire, c'est à dire que chaque fois que l'on dessine un hexagone on sait dire a priori s'il peut paver le plan ou pas.
Il y a trois types d'hexagones qui pavent le plan.

• Les hexagones avec deux arêtes opposés parallèles et égales.  Il s'agit de tous les hexagones tels que a+b+c=360° et A=D (voir dessin).
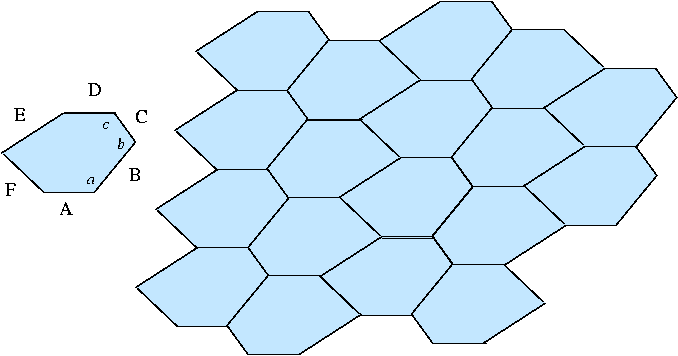
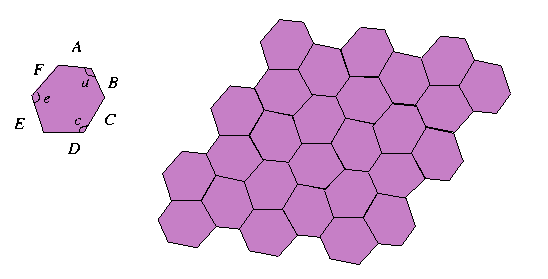
• En suivant la notation de l'hexagone ici-bas, il s'agit de tous les hexagones tels que A=B, C=D, E=F et a=c=e=120°.
• Les hexagones du type A=D, C=E, a+b+d=360°.

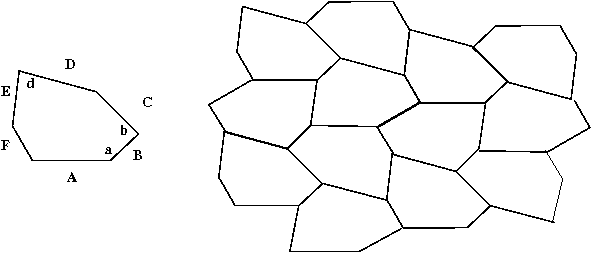
En mathématiques à la place du terme intutif type on prefère le mot classe.
Question: y-a-t'il un hexagone qui vie dans les trois classes, c'est-à-dire qui ont toutes les propriétés ci-dessus?

...mais les pentagones ?

Et pour les pentagones ? Le problème est ouvert, c'est à dire que on connaît quatorze classes de pentagones qui peuvent paver le plan, mais on ne sait pas si cette liste est exhaustive, c'est-à-dire si on a " laissé " dehors des pentagones qui peuvent donner des pavages du plan. Dans [1] on montre un exemple pour toute classe. Voici quelques exemples.