Peut-on paver ?
Carreleur > Polygones > Problemes ouverts > Heesch > Pentagones Mysterieux > Maths vs Physique > Bibliographie
A vous de voir si paver est toujours possible
Question : peut-on paver le plan avec ce polygone ? Intuitivement, quel serait votre avis ? Réponse

Et avec celui-ci ? Réponse
Procédons pas à pas
un, deux, trois, quatre...
Dans la quête de polygones qui peuvent paver le plan, le chemin le plus simple consiste sans doute à progresser au rythme du nombre de cotés des polygones. Avec un et deux c'est simple : il n'existe pas de polygone avec un ou deux cotés! Passons donc directement à trois et quatre cotés. Quels sont donc les triangles et les quadrilatères qui peuvent paver le plan? La première gageure est d'assembler à partir d'un élément de base choisi (triangle ou quadrilatère) un dessin, dit module dans le langage mathématique, susceptible de se répéter à l'infini pour paver le plan périodiquement (voir la démarche du test intuitif).

Essayez de trouver avec le triangle et le quadrilatère ici-bas des modules que l'on peut répéter, en obtenant ainsi un pavage périodique.
Et si vous ne le trouvez pas voici une aide.
Comme on peut imaginer, ce qu'on a vu pour ce triangle et ce quadrilatère est bien vrai pour tout triangle et tout quadrilatère, c'est à dire que tout polygone avec au plus quatre arêtes peut paver le plan d'une façon périodique. Démontrer cette assertion ne demande pas beaucoup d'outils mathématiques ([5]).
...cinq, six...
Poursuivons notre comptage et passons aux polygones avec cinq arêtes (les pentagones) et six arêtes (les hexagones). Eh bien, ce n'est pas si simple, même pour les mathématiciens : ça mérite une page en soi !
...sept, stop !
Un autre résultat sur les pavages composés d'un seul type de polygone est que tout polygone convexe avec plus de six arêtes ne peut pas paver le plan. Cette démonstration est bien plus compliquée que la précédente et demande des connaissances mathématiques.
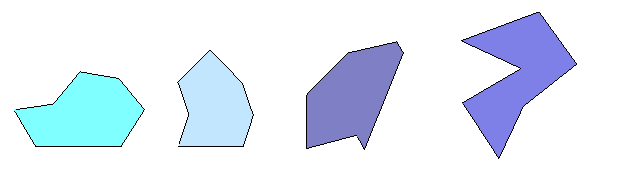
D'autre part, il est simple de trouver des polygones à sept arêtes (ou plus) qui ne sont pas convexes et qui pavent le plan. En voici quelques-uns, qui ont été trouvés tous avec la même règle... laquelle?