Heesch

Couronnes

Une question que l'on peut se poser quand on a un polygone qui ne peut pas paver le plan est de savoir au plus combien de fois le polygone peut être entouré complètement par des copies de lui même.

Avec un langage plus formel, supposons de prendre un polygone et de commencer à l'entourer avec des copies de lui même. Si on arrive à entourer entièrement (sans trous) le polygone, on appelle cet ensemble de polygones la première couronne du polygone donné. Une deuxième couronne sera un ensemble de polygones qui sont adjacents à la première couronne et qui l'entourent entièrement, et ainsi de suite...

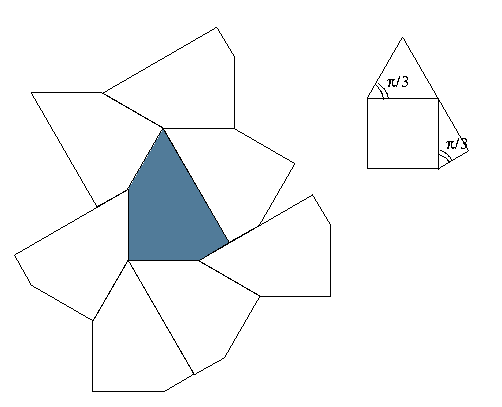
On appelle nombre de Heesch d'un polygone, le plus grand nombre k de couronnes que l'on peut construire à partir d'un polygone donné. Si le polygone de départ peut paver le plan (un carré, un hexagone régulier...) son nombre de Heesch sera infini, mais quand le polygone ne peut pas paver le plan, qu'est-ce qu'on peut dire? Le pentagone suivant par exemple a nombre de Heesch 1...

... et cet hexagone " dentellé " a (ou mieux, " avait ") nombre 3. Ce dernier a été découvert par le mathématicien Amman dans les années soixante-dix et pour de années a été l'exemple de polygone avec le nombre de Heesch le plus grand.

Dernièrement on a découvert des polygones (bien) compliqués avec nombre de Heesch 4 et 5, mais on a fait bien plus ; l'année dernière on a montré que l'exemple donné par Amman avait en réalité nombre 4 !

Problème de Heesch

Le problème de Heesch consiste à trouver, si elle existe, une borne supérieure pour les nombres de Heesch, ou, plus généralement, trouver les nombres qui, comme 1,2,3,4,5 (et l'infini) sont des nombres de Heesch pour quelque polygone.

Domino!

Le problème de Heesch est relié à un autre problème ouvert, le problème du domino. Le problème du domino demande s'il y a un algorithme que, donné un polygone, puisse décider si tel polygone pave le plan ou pas. Si le nombre de Heesch était fini, on pourrait effectivement construire tel algorithme...mais le sujet est assez compliqué et demande de connaissances en logique et en informatique. Une bonne référence pour tout qui concerne Heesch est la suivante [2].