Maths versus Physique

Combien de pavages ?

Un autre aspect intéressant quand on a un polygone, ou un ensemble de fini de polygones différents, qui peuvent paver le plan, c'est de analyser l'ensemble de pavages acceptés par le polygone ou l'ensemble de polygones de départ, donc en particulier de comprendre combien et quel type de pavages l'on pourrait obtenir. C'est une question naturelle, on a des briques et l'on veut savoir combien de " maisons " différentes l'on peut construire.

Pour le cas du carré (et le triangle équilatère et l'hexagone) la réponse est simple; si l'on demande des collages "arête contre arête" (les plus naturels) est immédiat montrer qu'il existe un seul pavage, l'échiquier infini, qui est périodique.

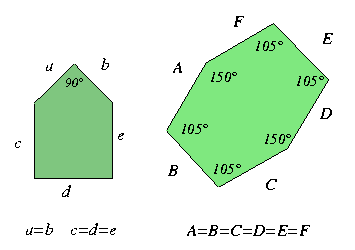
• Combien de pavages sont accepté par ce pentagone, en demandant des collages " arête contre arête "?
• Et par cet hexagone ?
• Pour le pentagone il y en a ...

Aperiodicité...un autre problème ouvert !

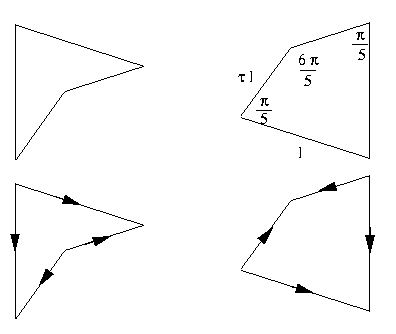
En général le problème de connaître combien et quel type de pavages on peut obtenir à partir d'un polygone (ou un ensemble de polygones) est très compliqué et le paysage des possibilités est incroyablement grand. En particulier, il y a une trentaine d'années, on a découvert les suivantes deux quadrilatères (appelés "cerf-volant" et "fléchette" ), pour lesquels, si on impose de ne coller deux pièces que lorsque que les flèches sont respectées, il existe un nombre infini de pavages différents qui ne sont jamais périodiques.

Voici une portion de pavage.

Des ensembles de polygones qui admettent que des pavages non périodiques, sont appelés apériodiques. Le problème ouvert, le plus fameux dans le monde de pavages est de trouver un polygone apériodique, c'est à dire un polygone qui peut paver le plan, mais jamais avec des pavages périodiques. Ce problème est strictement lié au problème de Heesch.

Seulement un jeu ?

Les exemples d'ensembles apériodiques que l'on connaît montrent des surprenants propriétés, en particulier des symétries " cachées" ([3], [4]). L'étude de l'apériodique est né comme un simple divertissement mathématique, et tel il est resté jusqu'aux années quatre-vingt quand on a découvert des matériaux avec des quasi-symétries analogues aux pavages apériodiques. Tels matériaux, qui ont pris le nom de " quasi cristaux " ([7])  ont bouleversé l'étude de la matière et ont donnée un nouvel élan à l'étude et à la compréhension profonde du phénomène de l'aperiodicité.